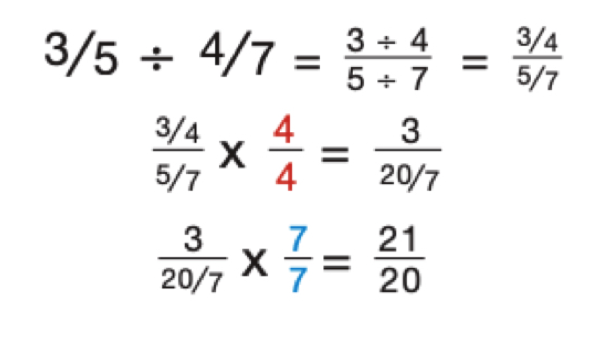There’s no question that dividing fractions is one of the topics about fractions that tends to cause more problems to students. The reality is that dividing fractions may be a bit tricky and we are the first ones to acknowledge this fact. After all, when you need to sum or subtract functions, all you need to keep in mind is that the fractions need to have the same denominator.
Make all the calculations you need with fractions here.
Dividing Fractions
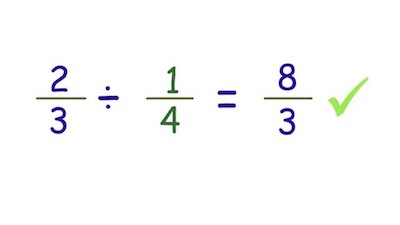
The main rule for dividing fractions requires that you use the reciprocal. But what does this mean exactly?
Simply put, using the reciprocal means that you need to flip the fraction over or invert it. Just to give you a simple example before we proceed, the reciprocal of 5/7 is 7/5.
So, here’s the entire process that you need to follow anytime you need to dividing fractions.
Make sure to use our simple calculator to divide fractions.
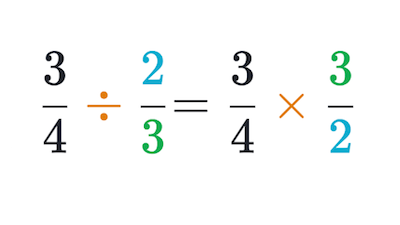
The truth is that in order to divide fractions, you need to convert the process into a multiplication by following the next steps:
Step #1: Change the division sign “÷” to the multiply sign “x” and invert the number to the right of the sign.
Step #2: Multiply the numerators.
Step #3: Multiply the denominators.
Step #4: Re-write your answer in its reduced or simplified form if needed.
One of the ways that we believe are best to understand any math concept is by showing you an example. This way, you can see how we put the steps into action and how you can do it on your own as well.
Discover why you learn functions.
Let’s imagine that you want to make the following division:
1/2 ÷ 1/3
So, as we mentioned in step #1, the first thing that you will need to do is to change the division sign into the multiply sign and invert the fraction on the right side of the signal. This means that you’ll end up with the following:
1/2 x 3/1
And now, you can simply proceed with the rules of multiplication:
1/2 x 3/1 = 3/2
And your simplified answer is: 1 1/2
Dividing Fractions By Whole Numbers
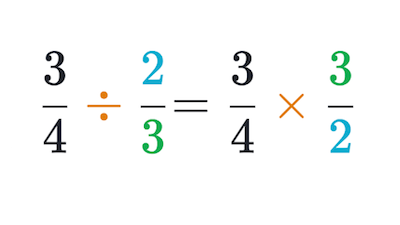
Let’s now imagine that you want or need to divide a fraction by a whole number:
1/2 ÷ 5
As you know, 5 = 5/1. So, if you apply the step#1 procedure:
1/2 x 1/5
Now, by applying the multiplication rules for fractions, you end up with:
1/2 x 1/5 = 1/10
Dividing Whole Numbers By Fractions

And what about the opposite: dividing whole numbers by fractions?
Well, the process continues to be exactly the same as the one we mentioned above.
Imagine that you need to calculate the following:
8 ÷ 1/3
As you know, 8 = 8/1 since 8÷1=8
So, this means that to apply the first step of the process, you will need to:
8 ÷ 1/3 = 8/1 x 3/1
Now, by applying the multiplication rules of fractions:
8/1 x 3/1 = 24/1 = 24
Bottom Line
As you can see, when you need to divide fractions, you just need to keep the process we detailed above in mind and follow it.