There’s no question that when you are learning fractions, there are many different topics that need to be covered.
Check out our fraction calculators.
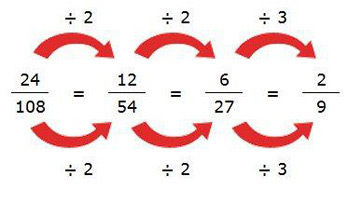
Between proper and improper fractions to mixed fractions, adding, subtracting, dividing, and multiplying fractions, and you can’t also forget about simplifying and reducing fractions.
What Is To Reduce Fractions?
Simply put, reducing fractions simply means that you are expressing the exact same fraction in a different way, generally in its simplest form. However, reducing it or not depends ultimately on what you want to do with it.

Here’s an example. Imagine that you are given some lengths that you need to compare and say which is the largest one or which is the smallest one. The lengths are:
1/2, 3/4, 6/16, 11/32
By looking at these fractions as they are, you may have no idea about which is the largest or the smallest length. However, if you reduce fractions, then it may help you get your answer. After all, if you reduce them to the same denominator, you would have:
16/32, 24/32, 12/32, 11/32
This makes it a lot easier to get your final answer.
Learn more about simplifying fractions.
Let’s now take a look at a different example to see if it makes sense to reduce fractions or not.
When you are driving or just on the bus, you may have already seen that road signs often follow a sequence like this:
1/10 mile
2/10 mile
3/10 mile
4/10 mile
5/10 mile
As you can see, these fractions aren’t reduced. In fact, if you needed to reduce them, the road signs would appear the following way on the road:
1/10 mile
1/5 mile
3/10 mile
2/5 mile
1/2 mile
As you can see, these fractions wouldn’t be so intuitive. So, in this case, we just don’t reduce fractions.
Understanding the pros and cons of fractions vs decimals.
Advantages Of Reducing Fractions
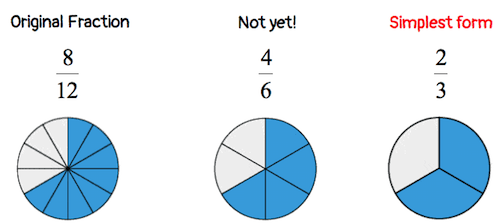
While there are many advantages that you can get from reducing fractions, there are two that stand out:
#1: You start to remember their decimal equivalents:
When you work with some fractions for some time, it is normal that you immediately know their decimal equivalents and even percentages. This can help you get some answers to your math problems in an easier and faster way.
Some examples of these fractions include:
1/2 = 0.5 = 50%
1/3 = 0.333… ~ 33%
1/4 = 0.25 = 25%
1/5 = 0.20 = 20%
1/8 = 0.125 = 12.5%
This is how you decompose fractions.
#2: Reducing fractions can help avoid miscommunications:
When you need to compare your answers with someone else, no matter if it is a colleague, a fellow student, a teacher, or even an automatic grading machine, then reducing fractions definitely prevents miscommunications. After all, there are many different ways o express any fraction; there’s not only one way.
Bottom Line
As you can see, reducing fractions is not difficult and it can certainly bring advantages. However, it is also important to keep in mind your goal. As we saw with the road signals, reducing fractions isn’t a good idea since you won’t get such a precise information.





