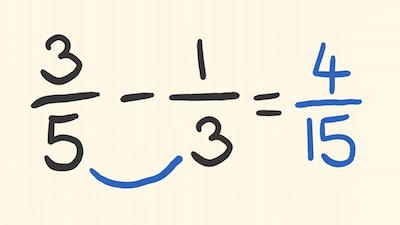No matter if you are just starting to take a closer look at percentages, the truth is that they can be quite useful in our lives.
Learn all about fractions here.

Imagine that your math teacher asks you to choose the bigger fraction from 3/4 and 7/8. What would you say? The reality is that you probably had no idea. However, if your teacher asked you to choose a bigger value from 75% and 87.5%, it becomes simple and easy. As you can see, the main difference is expressing the same number in terms of fraction or percentage. After all, they are the same. However, percentage values are easier than fractions to interpret.
Interpreting Percentages
Simply put, a percentage is just a number without a dimension or unit denoting a fraction of 100. So, you can then state that percentage means per hundred. It implies that a percentage value is the numerator value of a fraction with the denominator as 100. Besides, it is denoted by the % symbol.

So, 20 % is nothing but 20 parts per 100 which can also be written as 20/100 = 1/5. Therefore, the percentage value can be interpreted as a fraction by dividing the value by 100.
Learn how to add fractions with our free calculator.
Similarly, to convert a fraction into a percentage, you need to multiply and divide the fraction by 100 to make it into an equivalent fraction with the denominator as 100. This denominator value takes the form of %.
Note that the sum of percentages of different possibilities within a given problem/case can never be more than 100.
Here’s an example. Imagine that you want to convert the fraction 3/5 into a percentage. All you need to do is:
3/5 X 100/100 = 3/5 X 100% = 60%
Check out our fraction to percentage calculator.
Applying Percentages In Real Life

#1: Knowing “How Much” Or “How Many” Using Percentage:
A percentage value helps in calculating exactly what’s the amount or figure someone is talking about. For example, let’s say that Joe is spending 60% of his salary; it implies that Joe is spending $60 for every $100 he has been earning. So, how much Joe is actually spending if his salary is $60,000 per month?
You know that Joe spends 60% of his salary. Replacing 60% by 60/100 for calculating the amount, therefore, the amount Joe is spending = 60/100 X 60,000 = $36,000
#2: Comparing Fractions:
Fractions can be converted into percentages so you can easily compare them. This is particularly useful when the denominator values of two fractions are not the same. For example, John ate 3/5th of a pizza and Danny ate 5/8th of the other pizza of similar size. So, if we have to find who ate more, we need to compare by simply converting fractions into the percentage.
- John ate 3/5 X 100 = 60% of the pizza
- And Danny ate 5/8 X 100 = 62.5% of the pizza
As we convert the ratios into percentages, it becomes instantly clear that Danny ate more pizza than John.
Discover our percent to fraction calculator.
#3: Finding Percentage Increase Or Decrease:
This application of using percentages is particularly important in analyzing or comparing performances and progress. This is even more useful when the base criterion of comparison is different. For example,let’s say that in the mid-term exam, Ryan scored a total of 310 out of 500.
In the finals, he scored 430 out of 500. Clearly, the marks scored in the finals are higher than the ones scored in the mid-term exams. Therefore, there is an increment in the performance with the base value of 500.
Change in the performance / The base value X 100 ⇐ denotes the percentage change
Here, the increment in the performance = 430 – 310 = 120.
∴ Percentage increment = 120/500 X 100 = 24%