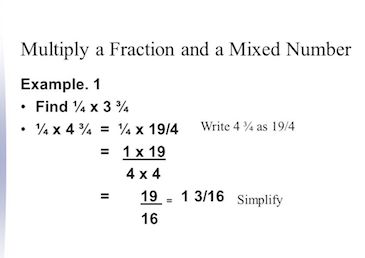Fractions don’t need to be complicated. After all, if you think about fractions, you can easily understand that they are no more or no less than a decimal number expressed in a different way where you have a numerator and a denominator.
Learn how to calculate fractions.

However, the truth is that many people struggle with fractions, especially with mixed fractions.
What Is A Mixed Fraction?
Simply put, a mixed fraction or mixed number as it is also known, is a number that combines a whole number and a fraction.
Discover more about multiplying fractions and mixed numbers.
How To Divide Mixed Fractions
Now that you already know what a fraction is and what a mixed fraction is, it is time to learn how to divide mixed fractions.
Simply put, if you know how to divide regular fractions, then you should have no problems with this calculation. However, before you start dividing mixed fractions, there is a step that you need to complete first: you need to convert the mixed fraction into an improper fraction first. Only when the mixed numbers are converted is that you can then go ahead and divide as you would divide any other fractions.
This is how you add and subtract mixed fractions.
Divide Mixed Fractions – The Steps
In order to ensure that you know exactly what to do when you want to divide mixed fractions, just follow the next steps:
Step #1: Convert the mixed fractions or mixed numbers to improper fractions.
Step #2: Divide as regular fractions using the formula for division of fractions:
a/b ÷ c/d = ad / bc
Step #3: Reduce fractions and simplify if possible.
Discover how to multiply fractions.
Divide Mixed Fractions – Example
Dividing mixed fractions is very similar to multiplying mixed fractions. You just add one step – after changing the divisor into an improper fraction, you then find its reciprocal and multiply. Let’s work through an example.
The SuperQuik Market has just installed new scanners for its check-out lanes. They claim the average time to check out a customer is 2 ½ minutes. How many customers, on average, can they check out in half an hour?
To solve this problem, you have to know that half an hour is the same as 30 minutes. Then you can divide 30 by 2 ½.
Step #1: Write the whole number and the mixed number as improper fractions:
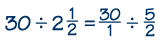
Step #2: Write the reciprocal of the divisor, 2/5, and multiply.
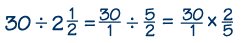
Step #3: Simplify, if possible. Notice that you can simplify this problem at this step, to make calculations easier. Five goes evenly into 30, so you can divide both 5 and 30 by 5, to give 1 and 6.
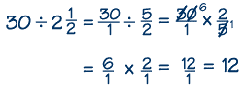
Step #4: Perform the simple multiplication of the numerators and the denominators. We find that the market can check out 12 customers in 30 minutes with its new scanners.
Step #5: Put the answer in lowest terms, and check the answer.
Since the answer is already in lowest terms, there is nothing left to do but check the answer, to be sure it makes sense. You can use estimation and rounding to do your check. If we round 2 ½ minutes to 3 minutes and divide 3 into 30, we get 10 customers in 30 minutes. So it is reasonable that 2 more customers per half hour, or 12 customers, can be checked, since 2 ½ minutes per customer is less than 3 minutes per customer.