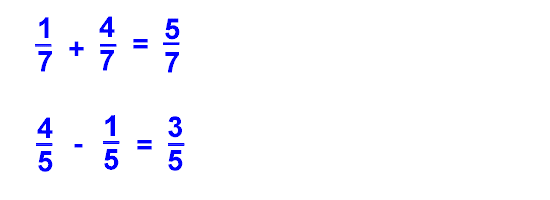Wonder how you compare fractions in the late elementary grades? In this post, we want to share a collection of methods that you can use to compare fractions.
In the past, we only learned one way to compare fractions. As time went by, we started to explore the different ways of representing and comparing fractions.
Check out the mixed fraction calculator

How to Compare Fractions In Grades 3-5
Below we have outlined 8 ways to compare fractions:
Equivalent Denominators
This is the easiest case in which to compare fractions. If two fractions have equivalent denominators, then compare the numerators to determine which fraction is greater. At the earliest stages of learning about fractions, students should be able to do this.
Equivalent Numerators
We were quite surprised to learn about this a few years ago. The fraction with the lesser denominator has a greater value if two fractions have equivalent numerators. The first time we heard this strategy, we were pretty certain that we disagreed with the person who told us it was possible! It is based on the idea that unit fractions with lesser denominators have a greater value than unit fractions with greater denominators [for example, 1/3 is smaller than 1/2]. This concept can be generalized to any fractions with common numerators—but we had to be convinced of this, as we had never learned it in grade school.
Check out the fraction calculator
Related Denominators
If two fractions have denominators that are easily related [like 4 and 8], then it is easy to rise one of them up quickly in order to compare them. This is especially useful when working with ruler measurement and line plots using halves, fourths, and eighths. Using measurement and data topics in Grades 3 to 5 is an essential way to support students’ reasoning about comparing fractions with denominators 2, 4, and 8.
Related Numerators
If two fractions have easily related numerators [like 3 and 6], then scaling the fraction with the lesser numerator to be equal to the greater numerator allows comparison based on their denominators. For example, to compare 3/4 and 6/7, scale 3/4 to be 6/8. It is easy to compare 6/8 and 6/7 if one knows that 1/7 is greater than 1/8.
Number Line Models
A great way to assess students’ comprehension of fractions is by subdividing a unit length on a number line in order to compare two fractions. Let students use whiteboards for constructions like these, as they can more accurately refine their subdivisions if required.
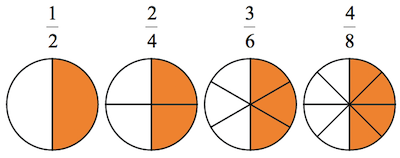
Area Models
In order to compare fractions, circles, squares, and rectangles are popular choices for subdividing. Teachers not only can assess students’ equal subdivisions, but also the idea of equally-sized unit wholes.
Use our percent to fraction calculator for free
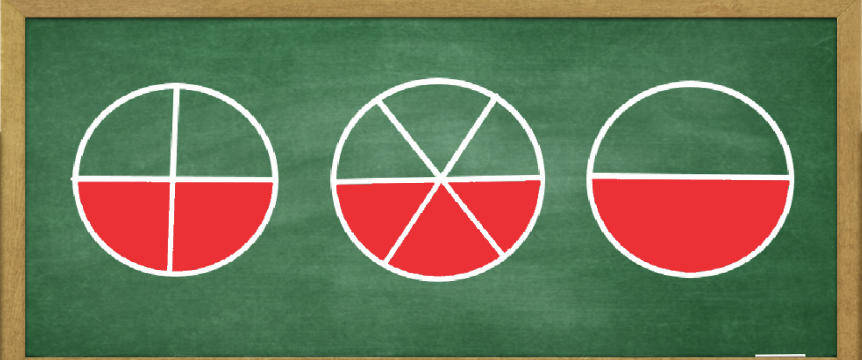
Benchmarks
Sometimes comparing fractions to benchmarks like 0, 1/2, or 1 is a fast way to compare fractions. For example, when comparing 5/9 to 6/13, students can exemplify their reasoning by stating that 5/9 is more than 1/2 while 6/13 is less than 1/2.
Cross Multiplication
The first fraction is greater than the second fraction if the product of the first numerator and the second denominator is greater than the product of the second numerator and the first denominator.
In Summary
As you can notice, students have many alternatives when comparing fractions. There are even more ways [converting to decimals, for example] that will become significant in later grades.