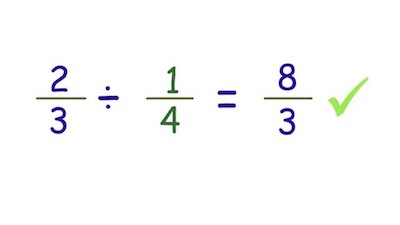There’s no question that a lot of students find fractions quite hard to understand. However, as long as you understand what fractions are, their purpose, and the rules for fractions, you can be sure that you won’t ever have any problem with fractions.

Discover everything you need to know about fractions.
What Is A Fraction?
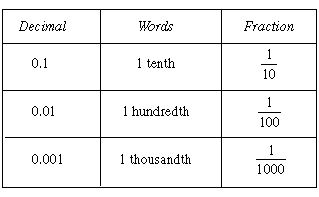
Simply put, a fraction is just a division expressed in a different way or even a decimal expressed in a different way. For example, it is the exact same thing if you have 0.1 or 1/10. And the reason is that the “/” in a fraction represents a division. So, this means that whenever you have a fraction, you can easily convert it into a decimal by simply dividing the numerator by the denominator.
Discover more about how to convert a fraction into a decimal.
Rules For Fractions
As we already mentioned above, as long as you are aware and understand the rules for fractions, you shouldn’t have any problems solving a problem with fractions. So, today, we are going to take a look at these rules.
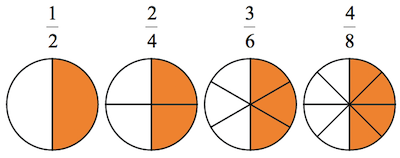
As you know, a fraction is just a part of a whole and it consists of a numerator and a denominator.
For example, let’s say that you have a cake and that you divide it into 8 equal parts. So, you can say that each piece is 1/8 of the cake.
Why you should use a fraction to decimal calculator?
#1: Adding And Subtracting Fractions:
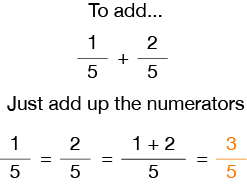
The main rule of adding and subtracting fractions is that both fractions need to have the same denominator. So, when you need to add or subtract fractions, you will first need to ensure that the denominators are the same, then add or subtract the numerators while keeping the denominator the same, and finally, reduce the answer whenever it is possible.
Here’s an example. Let’s say that you want to solve 1⁄4 + 1⁄4.
On this case, since the denominators are equal, you can simply add the numerators while maintaining the same denominator:
1/4 + 1/4 = 2/4
By looking at the fraction 2/4, you can easily see that it can be simplified this way:
2/4 = 1/2
But what if you have different denominators? Well, in this case, you will need to make the denominators the same first, and only then perform the calculations. Let’s take a look at an example.
Imagine that you want to solve 1⁄4 + 1⁄2.
As you can see, you have different denominators. So, you will need to change the denominator 2 and make it 4 by multiplying it by 2. However, notice that you need to multiply the numerator and denominator both by 2 to keep the value of the fraction unchanged.
Multiplying: 1⁄2 ✕ 2⁄2 = 2⁄4
Now, both denominators are the same which means that you can make the sum:
1/4 + 2/4 = 3/4
Notice that these rules apply to the subtraction as well.
Learn more about the relationship between fractions, decimals, ratios, and percentages.
#2: Multiplying Fractions:
To multiply two fractions, you simply multiply the numerators and denominators. Let’s take a look at a simple example. Imagine that you want to know the answer to 2⁄3 ✕ 3⁄15.
The first thing that you need to do is to simplify the fraction 3⁄15 to its lowest term:
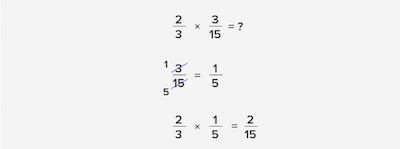
#3: Dividing Fractions:
Whenever you need to divide fractions, then you need to consider that some rules apply:
- Inverse the second fraction, that is, interchange its numerator and denominator to get the reciprocal.
- Multiply the first fraction by the reciprocal of the second fraction.