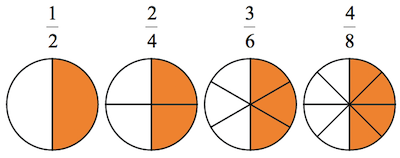
We understand that fractions may not be easy for the first time you look at them. The reality is that many math students keep struggling with fractions simply because they failed to understand its basics.

Simply put, a fraction is nothing more nor something less than a division. The number at the top is called the numerator and the number at the bottom is called the denominator. So, when you have the fraction 9/7, this is the same as stating that 9÷7.
Now that you understand the concept of fractions, then we can move on to learn how to multiply fractions.
How To Multiply Fractions
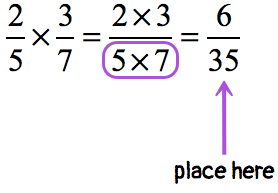
Simply put, whenever you need to multiply fractions, you just need to follow 3 simple steps:
Step #1: Multiply the numerators (or top numbers)
Step #2: Multiply the denominators (or bottom numbers)
Step #3: When it’s needed, we need to simplify or reduce the fraction.
One of the main differences between adding fractions and multiplying fractions is that you don’t have to reduce them to the same denominator. You can simply multiply them as they are, even when they have different denominators.
Check out our multiplying fractions calculator.
Let’s check an example. Let’s say that you want to know the result of 2/6 x 9/16.
So, you will need to follow the steps that we mentioned above:
Step #1: Multiply the top numbers (numerators):
2 x 9 = 18
Step #2: Multiply the bottom numbers (denominators):
6 x 16 = 96
So, at the moment, we have:
2/6 x 9/16 = 18/96
Step #3: Simplify the fraction:
18/96 dividing by 3, you get: 6/32
If you divide the fraction by 2, you get: 3/16
Learn more about simplifying fractions.
Multiplying Fractions With Whole Numbers

Multiplying whole numbers and fractions may stump your students because it seems that there is only one fraction and not 2. So, it is important to keep in mind that you can transform any whole number into a fraction. For example, 4 is exactly the same as 4/1. With this in mind, we believe that you won’t ever struggle when you need to multiply a fraction by a whole number.
Let’s take a look at an example. Imagine that you want to know the result of 2 × ⁵⁄₁₃.
The first thing that you need to do is to rewrite the whole number as a fraction:
²⁄₁ × ⁵⁄₁₃
Now, you just need to follow the same steps described above:
#1: Multiply numerators: 2 × 5 = 10
#2: Multiply denominators: 1 × 13 = 13
#3: New fraction: ¹⁰⁄₁₃
Multiplying Improper Fractions

Simply put, there is no difference in terms of multiplication of proper and improper fractions. Nevertheless, when some students see an improper fraction, they simply block. So, let’s take a look at a practical example.
Let’s say that you want to know the result of ⁵⁄₃ × ⁷⁄₆.
Again, you just need to follow the previous steps:
#1: Multiply numerators: 5 × 7 = 35
#2: Multiply denominators: 3 × 6 = 18
#3: New fraction: ³⁵⁄₁₈