Working with fractions is not easy for some people. For others, it’s quite simple unless they need to divide fractions.
Discover everything you need to know about fractions.
The reality is that if you are trying to teach your students how to divide fractions, you can tell them that it can be as simple as multiplying them. However, it is also important they understand the problem and the result and not only can learn how to divide fractions.
How To Divide Fractions
If you simply divided fractions like you were dividing a normal math problem, you’d more than likely create some complex fractions and have something that looks similar to this:
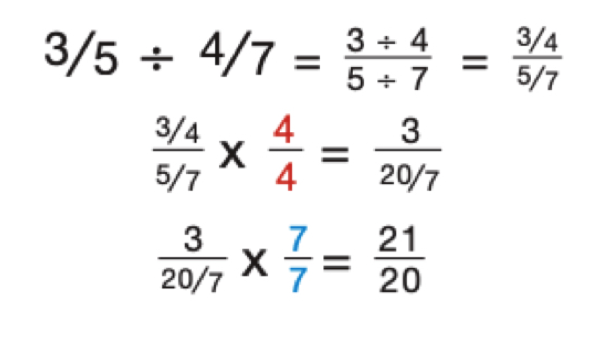
That’s not exactly an easy process to follow. Fortunately, there’s a shortcut you can use that makes dividing fractions much simpler. You can solve most division problems by following these three steps:
- Flip the divisor into a reciprocal
- Change the division sign to a multiplication symbol and multiply
- Simplify your answer if possible
These steps streamline the dividing process and help you avoid complex fractions.
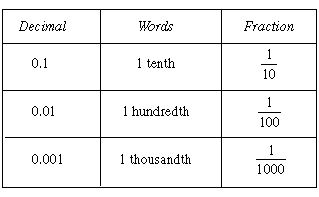
Discover the importance of decimals.
Step 1: Flip the divisor into a reciprocal
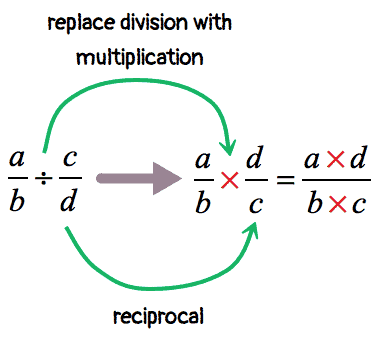
A reciprocal is what you multiply a number by to get the value of one. If you want to change two into one through multiplication you need to multiply it by 0.5. In fraction form this looks like:
²⁄₁ × ½ = 1
To find the reciprocal of a fraction you simply flip the numbers. The denominator becomes the numerator and vice versa.Take a look at the example equation again:
½ ÷ ⅙ = ?
The first step to solve the problem is to turn our divisor, ⅙, into a reciprocal.
⅙ → ⁶⁄₁
Learn how to convert between percents, fractions, and decimals.
Step 2: Change the division sign to a multiplication symbol and multiply
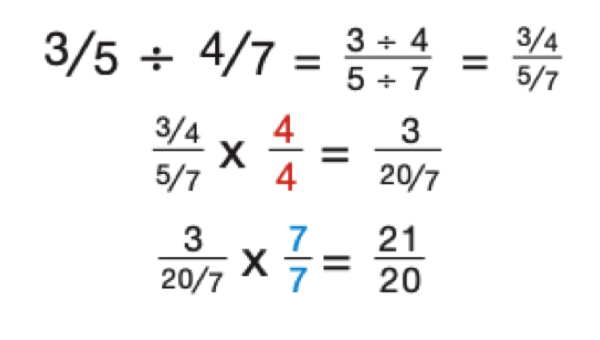
Dividing and multiplying are opposites of each other. When you create a reciprocal of a number, you’re creating its opposite as well. In a division problem, when you turn the divisor into a reciprocal, you also need to change the equation from division to multiplication. Now that you’ve found the reciprocal of your divisor, you can change the equation from division into multiplication.
½ ÷ ⅙ = ? → ½ × ⁶⁄₁ = ?
Now, to multiply fractions, you just need to:
- Multiply your numerators to get your new numerator
- Multiply your denominators to get your new denominator
- Simplify the final fraction, if possible
For the example equation you have two problems to solve:
1 × 6 = 6 2 × 1 = 2 ½ × ⁶⁄₁ = ⁶⁄₂
Now you’re ready to simplify to get the final answer!
Learn more about the uses of percentages.
Step 3: Simplify your answer if possible
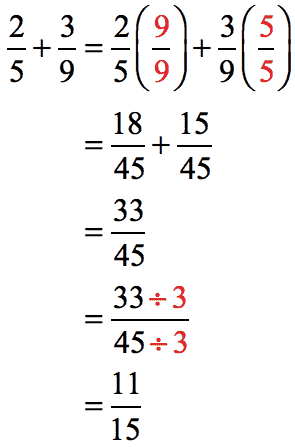
Fractions symbolize a part of a whole. This means many fractions represent the same value, so why not make the fraction as simple as possible?For example, you almost never say five-tenths or ⁵⁄₁₀. Instead, you simplify that to one-half or ½.To get a fraction down to its simplest form, you divide the numerator and denominator by their greatest common factor. The greatest common factor in ⁵⁄₁₀ is five. Dividing both numbers down by five leaves you with ½.
In the example question, the greatest common factor of ⁶⁄₂ is two. This turns your solution from ⁶⁄₂ to ³⁄₁, which is the same as saying three. Therefore:
½ ÷ ⅙ = ? → ½ × ⁶⁄₁ = ⁶⁄₂ → ³⁄₁ → 3