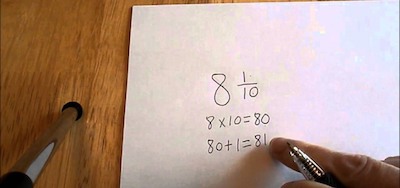While many students struggle with fractions, things tend to be even a bit more complicated when it comes to mixed fractions.
Discover the best fraction calculators.

The reality is that as soon as you understand the concept of mixed fractions, you should be just fine and you shouldn’t have any more problems when performing simple math operations such as adding or subtracting.
What Are Mixed Fractions?
Simply put, mixed fractions are just one type of fraction and it is also known as mixed numbers. Ultimately, this type of fraction includes a fraction and a whole number.

A simple example of a mixed fraction is 2(1/7), where 2 is a whole number and 1/7 is a fraction.
Discover how to multiply fractions.
Adding Mixed Fractions
As you probably already know, when you are looking to add fractions, you need to both have the same denominators.
To ensure that the calculations are easier, you should always change the mixed fractions to improper fractions first.
#1: Adding With The Same Denominators:
Example: 6/4 + 5/4
Step 1: Since the denominator of both fractions is the same (4), you can keep it.
Step 2: Add the numerators and maintain the same denominator:
6 + 5 =11
6/4 + 5/4 = 11/4
Step 3: If the answer is in improper form, you need to convert it into a mixed fraction:
11/4 = 2 (¾)
Understanding simplifying fractions.
#2: Adding With Different Denominators:
Example: 8/6 +12 /8
Step 1: As we already mentioned above, you need to first find the LCM between the denominators.
The LCM of 6 and 8 is 24
Step 2: Multiply both denominators and numerators of both fractions with a number such that they have the LCM as their new denominator.
So, in our example, you need to multiply the numerator and denominator of 8/6 with 4 and 12/8 with 3.
Step 3: Add the numerator and keep the denominators the same.
32 / 24 + 36 / 24
= 68/24 = 17/6
Step 4: If the answer is in improper form, convert it into a mixed fraction:
17/6 = 2 (⅚)
Discover everything you need to work with decimals.
Subtracting Mixed Fractions:

#1: Subtracting With Th Same Denominators:
Example: 6/4 – 5/4
Step 1: Keep the denominator ‘4’ the same.
Step 2: Subtract the numerators:
6 – 5 = 1
6/4 – 5/4 = 1/4
Step 3: If the answer is in improper form, you need to convert it into a mixed fraction.
In this case, there’s no ned since:
6/4 – 5/4 = 1/4
#2: Subtracting With Different Denominators:
Example: 12/8 – 8/6
Step 1: Find the LCM between the denominators:
The LCM of 8 and 6 is 24.
Step 2: Multiply both denominators and numerators of both fractions with a number such that they have the LCM as their new denominator.
Multiply the numerator and denominator of 8/6 with 4 and 12/8 with 3.
Step 3: Subtract the numerator and keep the denominators the same.
36 / 24 – 32/24 = 4/24
Step 4: If the answer is in improper form, convert it into Mixed Fraction:
4/24 = 1/6