You may be wondering why do we even need decimals. After all, we already have whole numbers. However, we have to say that whole numbers aren’t just enough.
One of the things that you may not know is that whole numbers are also called counting numbers for a reason. After all, they allow you to specify discrete quantities like when you say that there are 50 people in the movie theatre. These 50 people are separate entities. So, it doesn’t make sense to talk about them in any other way than using whole numbers. However, not all numbers are like this.

Learn everything you need about fractions.
The reality is that other quantities aren’t discrete but continuous. The height of people or the amount of cake you eat are continuous quantities. So, when you need to describe them, you need to use a basic measurement unit intermediate between two whole numbers that need to be specified and communicated.
The first way in which people solved this problem was to invent new smaller units. For example, the basic unit of time, the day, was divided into hours and then into minutes and then into seconds. Gradually people agreed that there would be 24 hours in a day and that the hours would be of equal length. The hour itself was divided into 60 minutes, which were again divided into 60 seconds. Today even smaller units of time are often needed, for example, to describe the race times of runners and swimmers or to keep communications through computers synchronized.

Discover the uses of percentage.
Measuring more and more precisely by creating smaller and smaller units has the advantage that only whole number arithmetic is needed. For example, problems about hours and minutes require only knowledge of whole numbers and the conversion 60 minutes = 1 hour. However, smaller and smaller units need to be invented and the conversions remembered. The metric system makes this easier, with all conversion factors based on ten.
The second solution to the problem of describing measuring more precisely is by extending the number system itself to include both common fractions and decimal fractions.
Understanding the relationship between decimals, fractions, and percentages.

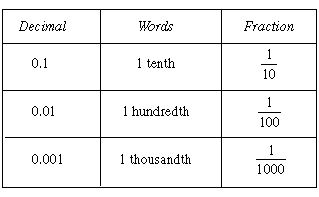
Using fractions or decimals, continuous quantities can be described to any desired accuracy:
- the area of the floor is thirty-six square metres and eight tenths of another square metre, that is 36 square metres, or 36.8 square metres, or more commonly, 36.8 m2
- the cost of carpet for a square metre is $40.35 (forty dollars and thirty-five cents), or forty dollars and thirty-five hundredths of another dollar, that is 40 dollars, or 40.35 dollars.
Discover when to reduce fractions.
Note that there are two units (the dollar and the cent) being used in the money example, but not in the area example. The area example shows that there is no need for the smaller unit (the tenth of a square metre) to have a name. The number system itself provides all the information required, because the whole number and fractional parts are not separate, but are together in the one number.
There are mathematical advantages to extending the number system rather than creating smaller units. This is not shown with addition and subtraction but with multiplication and division.